MATLAB绘图

函数

二维图像

二维笛卡尔坐标系 plot

plot函数具有不同的形式，具体取决于输入参数。

  • plot(x) 如果 x 是向量，plot(x) 会生成 x 元素与 x 元素索引的分段线图
  • plot(x,y) 如果有两个向量被指定为参数，plot(x,y) 会生成 y 对 x 的图形
单个函数图像

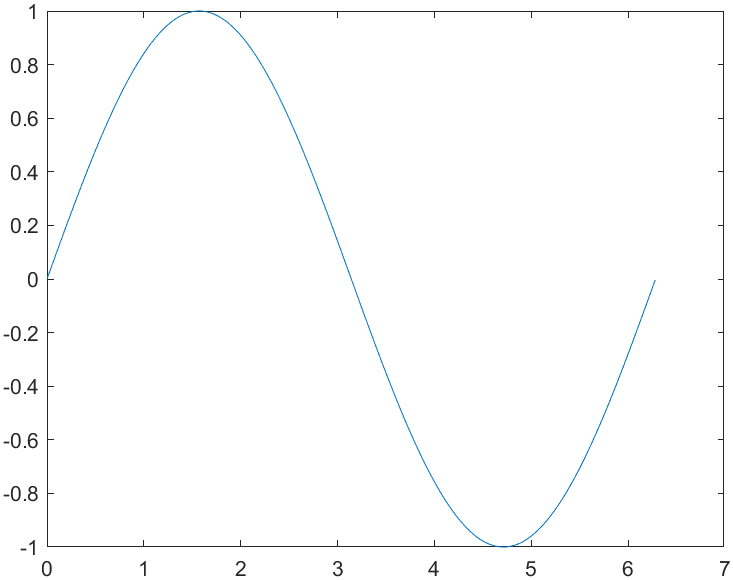
示例：正弦函数

x = 0:0.01:2*pi; % 创建一个从 0 到 2*pi 的向量，步长为 0.01，用于表示正弦函数的 x 轴上的点。  
y = sin(x);      % 计算 x 向量中每个点对应的正弦值，结果存储在 y 向量中。  
plot(x,y)        % 使用 plot 函数绘制 y 关于 x 的图形。

sin function-1

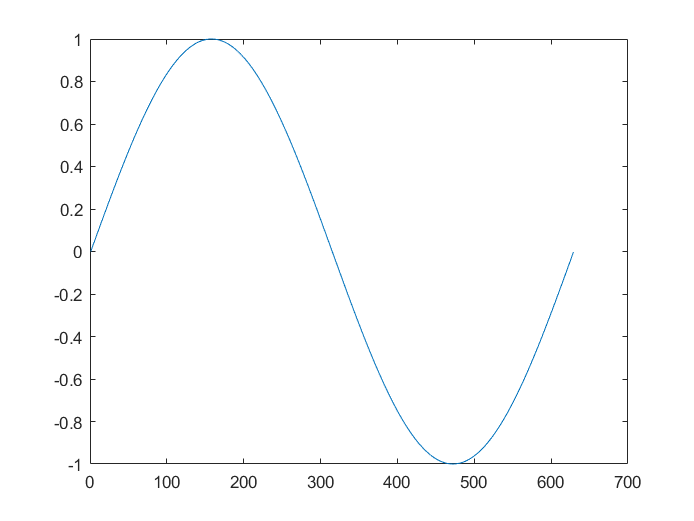
另一种写法

x = 0:0.01:2*pi;    % 创建一个从 0 到 2*pi 的向量，步长为 0.01，用于表示正弦函数的 x 轴上的点。  
plot(sin(x))        % 使用 plot 函数绘制 sin(x) 的图形，横坐标为点的序号

sin-function-3

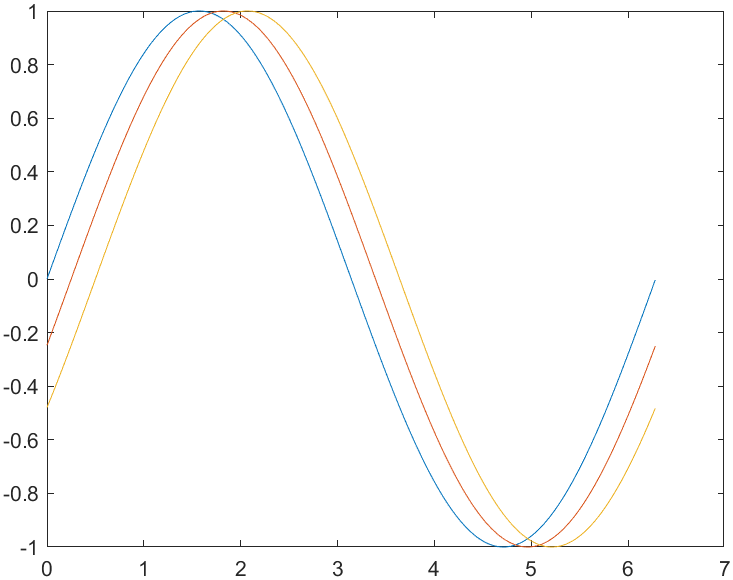
多个函数图像
x = 0:0.01:2*pi;       % 创建一个从0到2*pi的向量，步长为pi/100，用于表示x轴的值。  
y1 = sin(x);           % 计算x向量对应的正弦值。  
y2 = sin(x-.25);       % 计算相移-0.25后的正弦值。  
y3 = sin(x-.5);        % 计算相移-0.5后的正弦值。  
plot(x,y1,x,y2,x,y3)   % 绘制三个正弦波的图形。

sin function-2

另一种写法

用到 hold 命令

hold on

hold off

当命令键入时，MATLAB 不会在您发出其他绘图命令时替换现有图形，而会将新图形与当前图形合并在一起。

x = 0:0.01:2*pi;       % 创建x向量  
y1 = sin(x);           % 正弦函数  
y2 = sin(x-.25);       % 相移-0.25的正弦函数  
y3 = sin(x-.5);        % 相移-0.5的正弦函数  
  
% 绘制图形并为每条曲线指定颜色和图例  
plot(x,y1);     % 原始的sin(x)  
hold on;        % 保持当前图形，以便添加更多曲线  
plot(x,y2);     % 相移-0.25的正弦函数 
plot(x,y3);     % 相移-0.5的正弦函数 
hold off;       % 取消保持

双纵坐标函数 plotyy

plotyy(x,y1,x,y2)

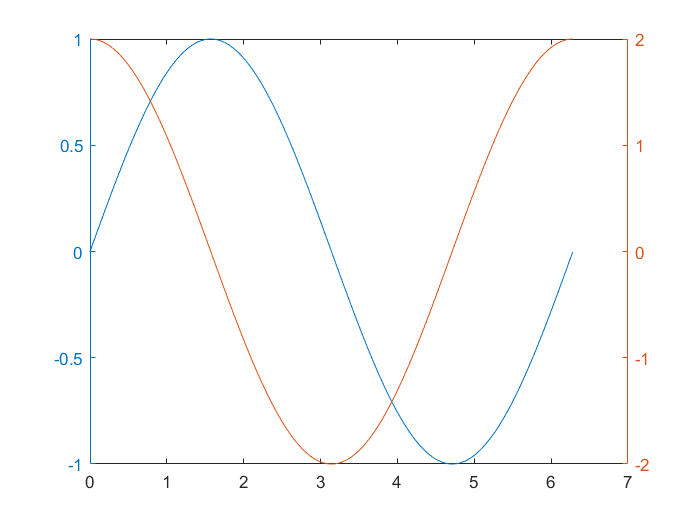
把具有不同量纲，不同数量级的两个函数绘制在同一个坐标中，有利于图形数据的对比分析

x = 0:0.01:2*pi;  % 定义x的范围，从0到2*pi，间隔为0.01 
y1 = sin(x1);     % 计算y1的值，y1是x的正弦函数 
y2 = 2*cos(x1);   % 计算y2的值，y2是x的余弦函数的2倍 
plotyy(x,y1,x,y2) % 使用plotyy函数绘制两个函数，左侧Y轴对应y1，右侧Y轴对应y2

trig function-2

图形窗口分割 subplot

subplot(m,n,p)

把当前窗口分成m×n个绘图区，m行 每行n个绘图区，区号按行优先编号 其中第p个区为当前活动区 每一个绘图区允许以不同的坐标系单独绘制图形

x = -pi:0.01:pi; % 创建一个从 -pi 到 pi 的向量，步长为 0.01，用于表示 x 轴上的点。 
y1 = sin(x);      % 正弦函数
y2 = cos(x);      % 余弦函数
y3 = tan(x);      % 正切函数，注意这将在 x = pi/2 + n*pi 处产生无穷大

% 为了避免在奇点处的绘图错误，我们可以将奇点附近的值设置为 NaN（不是数字）。  
% 这样，MATLAB 在绘图时会忽略这些值。
y3(abs(x) >= pi/2 - 0.01 & abs(x) <= pi/2 + 0.01) = NaN;  

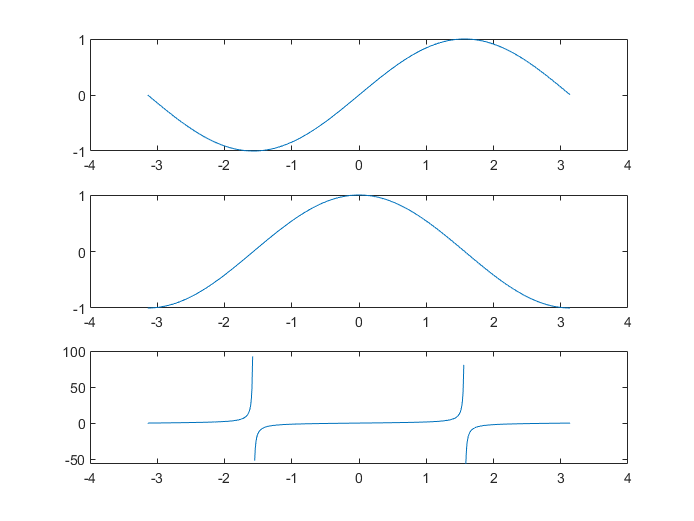
subplot(3,1,1);  % 将图形窗口分割为 3 行 1 列的子图网格，并激活第 1 个子图以供绘制。  
plot(x,y1)     % 在第 1 个子图上绘制 sin(x) 的图形。  

subplot(3,1,2);  % 激活第 2 个子图以供绘制。  
plot(x,y2)     % 在第 2 个子图上绘制 cos(x) 的图形。  

subplot(3,1,3);  % 激活第 3 个子图以供绘制。  
plot(x,y3)     % 在第 3 个子图上绘制 tan(x) 的图形。

trig function-1

极坐标系 polar

polar(theta,rho,'options')

polarplot(theta,rho,'options') MATLAB 建议使用 polarplot

theta 为极角，rho 为极径，选项 options 的内容与plot函数相同

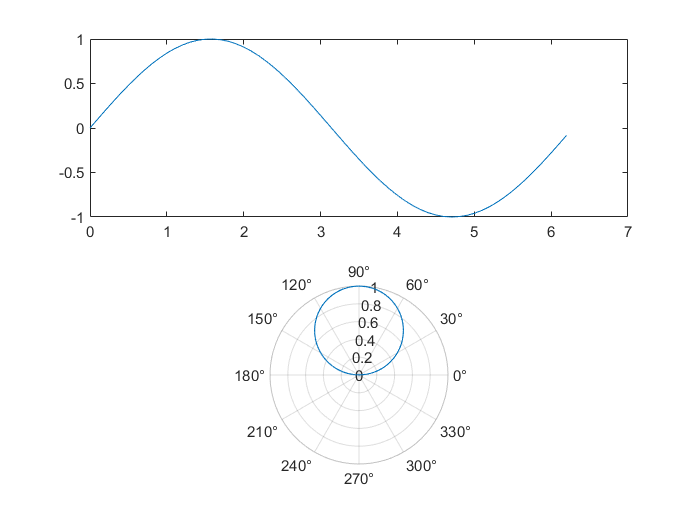
下面对 plot 和 polarplot 进行对比

theat = 0:0.1:2*pi;
y = sin(theat);
subplot(2,1,1);
plot(theat,y);
subplot(2,1,2);
polarplot(theat,y);

polar

对数坐标图 semilogx/semilogy/loglog

  • x轴线性，y轴线性

    plot(x,y)

  • x轴对数，y轴线性

    semilogx(x,y)

  • x轴线性，y轴对数

    semilogy(x,y)

  • x轴对数，y轴对数

    loglog(x,y)

% 创建一个从1到100的整数向量  
x = 1:100;  
  
% 根据x的值计算y的值，y是e的x次方  
y = x.^2+exp(x);  
  
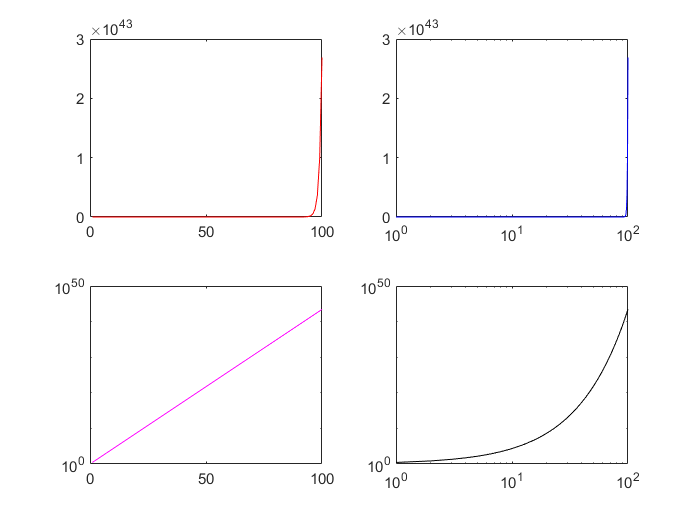
% 创建一个2x2的子图布局，并选择第一个子图位置进行绘图  
subplot(2,2,1)  
  
% 在当前子图上使用红色实线绘制x和y的关系图  
plot(x,y,'r-')  
  
% 选择第二个子图位置进行绘图  
subplot(2,2,2)  
  
% 使用半对数x轴（x轴为对数刻度，y轴为线性刻度）和蓝色实线绘制x和y的关系图  
semilogx(x,y,'b-')  
  
% 选择第三个子图位置进行绘图  
subplot(2,2,3)  
  
% 使用半对数y轴（y轴为对数刻度，x轴为线性刻度）和洋红色实线绘制x和y的关系图  
semilogy(x,y,'m-')  
  
% 选择第四个子图位置进行绘图  
subplot(2,2,4)  
  
% 使用对数坐标轴（x轴和y轴均为对数刻度）和黑色实线绘制x和y的关系图  
loglog(x,y,'k-')

log

符号函数 ezplot/fplot/flmplicit

注：在MATLAB的上下文中，当提到“符号函数”时，通常指的是使用Symbolic Math Toolbox中的符号计算功能来定义和操作数学表达式，而不是指特定的数学上的符号函数

ezplot

ezplot 函数会自动选择合适的 x 和 y 范围来显示整个函数图像。如果需要自定义范围，可以在调用 ezplot 时传递一个额外的范围向量。

ezplot 通常适用于绘制简单的函数图像。对于更复杂的函数或需要更高精度的图形，可能需要使用其他绘图函数，如 plot、fplot 或 surf 等，并手动处理数据的生成和图形的绘制。

在某些情况下，隐式方程可能难以或无法用 ezplot 准确绘制，特别是当方程具有奇点或复杂的几何结构时。在这些情况下，可能需要采用其他方法或工具进行绘图。

ezplot 函数的调用格式如下：

  • 隐函数

    ezplot('f(x)',[a,b])

    ezplot('f(x,y)',[xmin,xmax,ymin,ymax])

    [a,b]和[xmin,xmax,ymin,ymax]定义了自变量的取值范围。

  • 参数方程

    ezplot('x(t)','y(t)',[tmin,tmax])

    [tmin,tmax]定义了自变量的取值范围。

% 创建一个3行1列的子图布局，并选择第一个子图位置进行绘图  
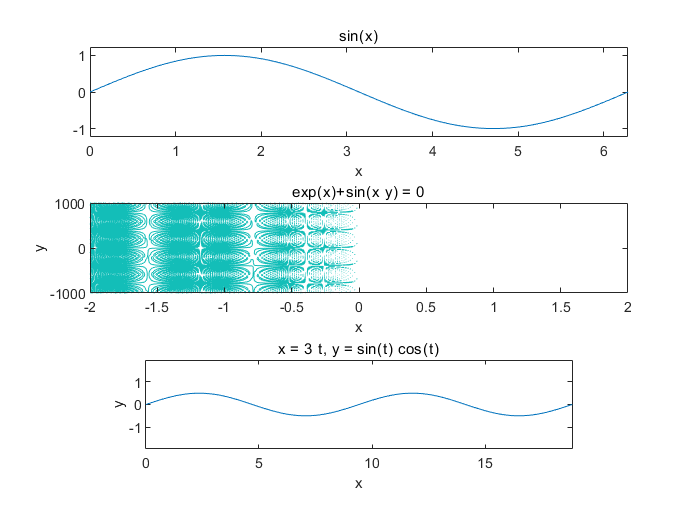
subplot(3,1,1)  
  
% 使用ezplot函数绘制正弦函数sin(x)的图像，x的范围从0到2*pi  
% ezplot是一个方便的函数，用于绘制隐式或参数形式的函数图像  
ezplot('sin(x)',[0,2*pi])  
  
% 切换到第二个子图位置进行绘图  
subplot(3,1,2)  
  
% 使用ezplot函数绘制函数exp(x)+sin(x*y)的图像  
% 这里的x范围从-2到2，y的范围从-1000到1000  
% 由于x和y的范围差异很大，可能得到的图像在y轴上看起来非常压缩  
ezplot('exp(x)+sin(x*y)',[-2,2,-1000,1000])  
  
% 切换到第三个子图位置进行绘图  
subplot(3,1,3)  
  
% 使用ezplot函数绘制参数方程定义的曲线  
% 这里，x由参数t通过表达式'3*t'给出，y由参数t通过表达式'sin(t)*cos(t)'给出  
% t的范围从0到2*pi  
% ezplot的参数形式通常使用两个字符串，第一个表示x与参数t的关系，第二个表示y与参数t的关系  
ezplot('3*t','sin(t)*cos(t)',[0,2*pi])

ezplot

fplot

fplot 函数是MATLAB中的一个函数，主要用于绘制由函数表达式定义的曲线。它特别适用于快速绘制函数的图形表示，无需显式地创建向量来表示函数的输入和输出。

fplot 函数的调用格式如下：

  • 对于单变量函数：

    fplot(fun, [xmin, xmax])

    其中，fun是一个函数句柄或函数表达式，表示要绘制的函数；[xmin, xmax]定义了自变量的取值范围。

  • 对于参数化曲线：

    fplot(fx, fy, [tmin, tmax])。

    其中，fx和fy分别表示x和y关于参数t的表达式；[tmin, tmax]定义了参数t的取值范围。

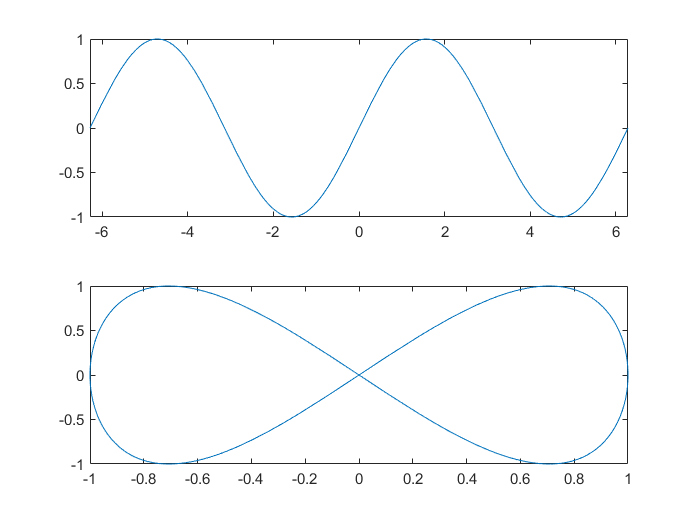
subplot(2,1,1)  
% 在 [-2*pi, 2*pi] 区间内绘制正弦函数   
fplot(@(x) sin(x), [-2*pi, 2*pi]);  
subplot(2,1,2)  
fplot( @(t) cos(t), @(t) sin(2*t), [0, 2*pi])

fplot

flmplicit

fimplicit是MATLAB中的一个函数，用于绘制二元函数的图像。无论是简单的函数还是复杂的函数，都可以通过fimplicit函数来实现。其基本语法如下：

fimplicit(f, [xmin xmax ymin ymax])

其中，f是一个二元函数，[xmin xmax ymin ymax]是绘图区域的范围。

使用fimplicit函数时，可以通过匿名函数或函数句柄来定义所需绘制的函数。此外，还可以定义自定义的范围来限制函数的绘图区域。

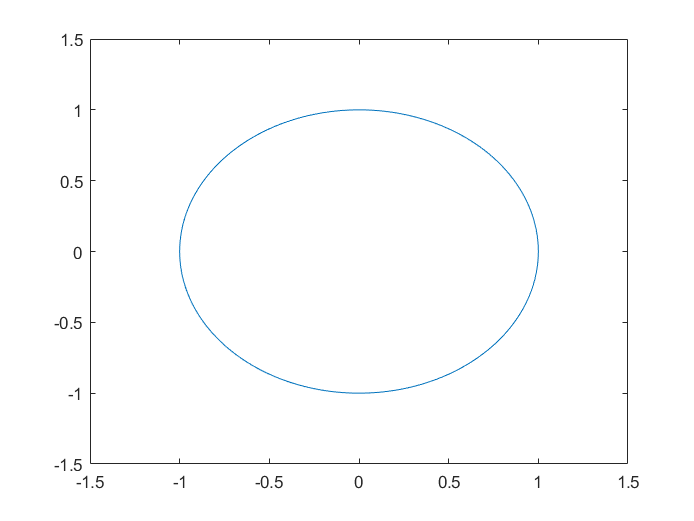
% 绘制由方程 x^2 + y^2 = 1 定义的单位圆的图像
fimplicit(@(x,y) x.^2 + y.^2 - 1, [-1.5 1.5 -1.5 1.5])

fimplicit

此外，fimplicit函数也接受更复杂的语法形式，比如：

fimplicit(@(varible)function, interval, Name,Value)

其中，varible是方程中全部的变量，function是确定隐函数的二元方程中左端项，interval表示方程中两个变量的区间，Name和Value分别表示图元的名称和属性值。

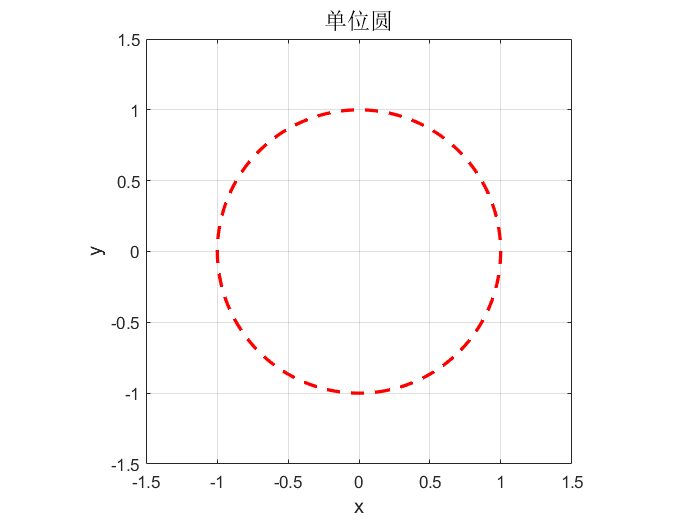
% 绘制单位圆的隐函数图像
% 通过Name,Value对设置了线型（LineStyle）为虚线（'--'），线宽（LineWidth）为2，颜色（Color）为红色（'r'）
fimplicit(@(x,y) x.^2 + y.^2 - 1, [-1.5 1.5 -1.5 1.5], 'LineStyle', '--', 'LineWidth', 2, 'Color', 'r')  
axis equal  
title('单位圆', 'FontSize', 14)  
xlabel('x', 'FontSize', 12)  
ylabel('y', 'FontSize', 12)  
grid on

fimplicit2

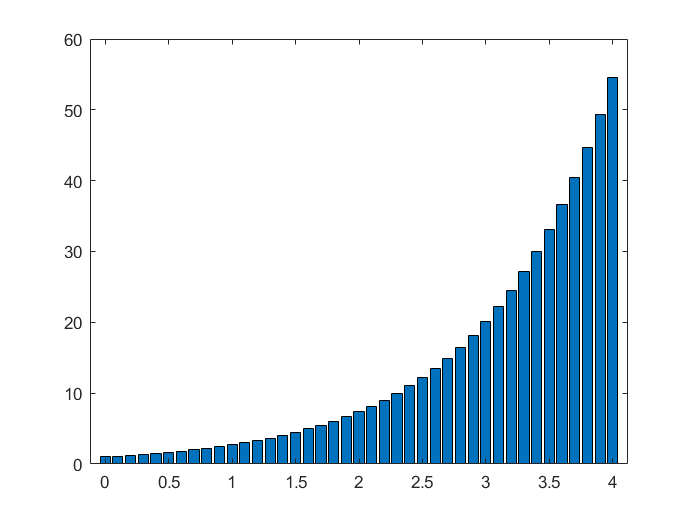
条形图 bar

bar(x,y)

x = 0:0.1:4;
y = exp(x);
bar(x,y);

bar

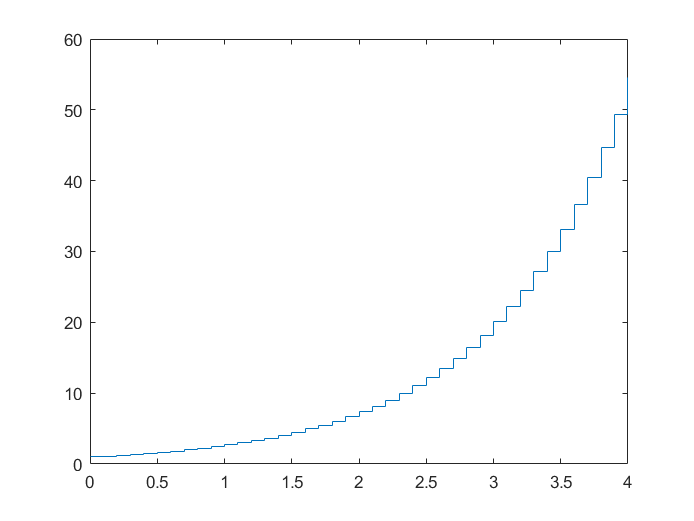
阶梯图 stairs

stairs(x,y)

x = 0:0.1:4;
y = exp(x);
stairs(x,y);

stairs

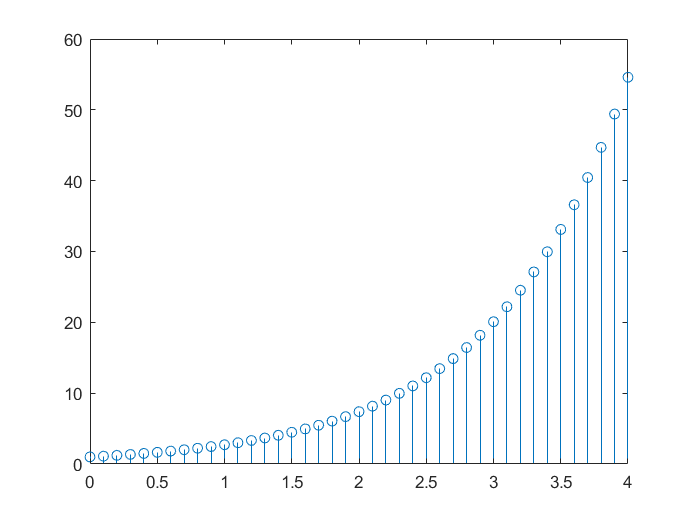
杆图 stem

stem(x,y)

x = 0:0.1:4;
y = exp(x);
stem(x,y);

stem

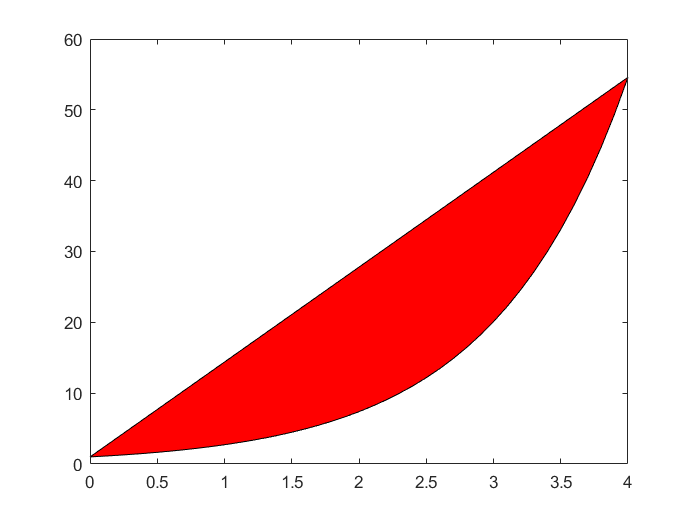
填充图 fill

fill(x,y,c1)

c1 为颜色，必须加上

fill 函数按向量元素下标渐增次序依次用直线段连接 x，y 对应元素定义的数据点

x = 0:0.1:4;
y = exp(x);
fill(x,y,'r');

fill

三维图像

空间曲线 plot3

plot3(x,y,z,'options')

用法和 plot 相似

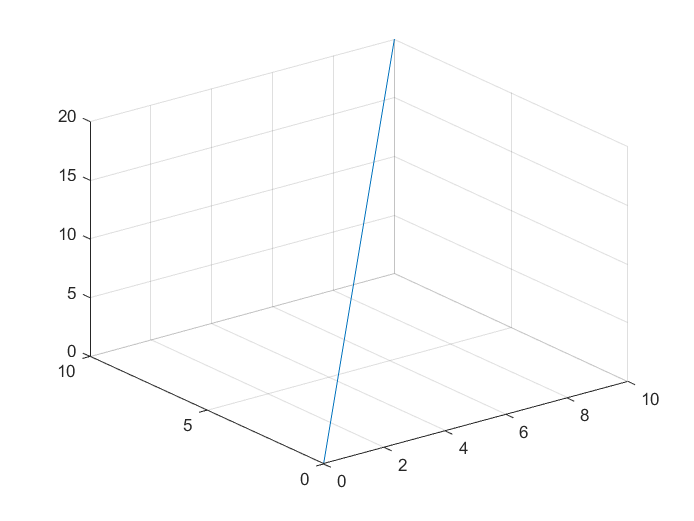
x = 0:0.1:10;
y = 0:0.1:10;
z = x+y;
plot3(x,y,z);
grid on;       #显示轴网格线

plot3

空间曲面 surf/mesh

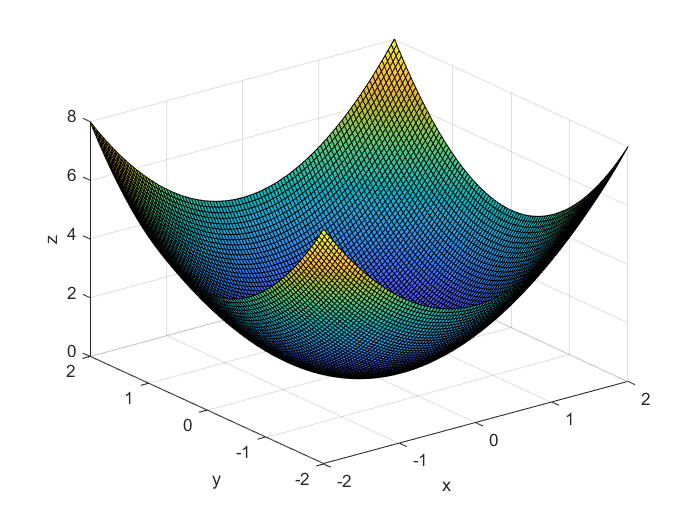
surf(x,y,z)

% 定义w和b的范围  
x_range = linspace(-2, 2, 100); % w的范围从-2到2，共100个点  
y_range = linspace(-2, 2, 100); % b的范围从-2到2，共100个点  
  
% 初始化三维网格  
[X, Y] = meshgrid(x_range, y_range);  
  
% 定义碗状函数  
Z = X.^2 + Y.^2;  
  
% 绘制三维图像  
figure; % 创建一个新的图形窗口  
surf(X, Y, Z); % 使用surf函数绘制三维曲面  
xlabel('x'); % 添加x轴标签  
ylabel('y'); % 添加y轴标签  
zlabel('z'); % 添加z轴标签

surf

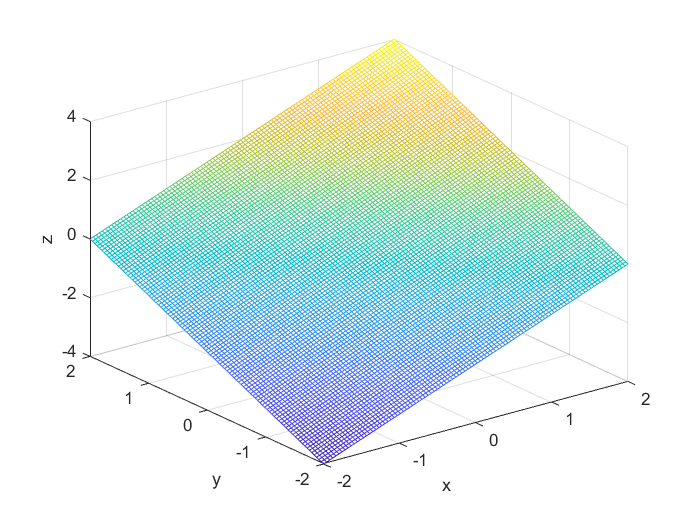
mesh(x,y,z)

% 定义w和b的范围  
x_range = linspace(-2, 2, 100); % w的范围从-2到2，共100个点  
y_range = linspace(-2, 2, 100); % b的范围从-2到2，共100个点  
  
% 初始化三维网格  
[X, Y] = meshgrid(x_range, y_range);  
  
% 定义碗状函数  
Z = X + Y;  
  
% 绘制三维图像  
figure; % 创建一个新的图形窗口  
mesh(X, Y, Z); % 使用surf函数绘制三维曲面  
xlabel('x'); % 添加x轴标签  
ylabel('y'); % 添加y轴标签  
zlabel('z'); % 添加z轴标签

mesh

mesh 和 surf 区别：

  • mesh 用于绘制不是特别精细的三维曲面网格图，同一层面的线条用相同的颜色表示

  • surf 用于绘制比较光滑的三维曲面网格图，各线条之间的补面用颜色填充

标准三维曲面 sphere/cylinder

Matlab提供了一些函数用于绘制标准三维曲面，这些函数可以产生相应的绘图数据

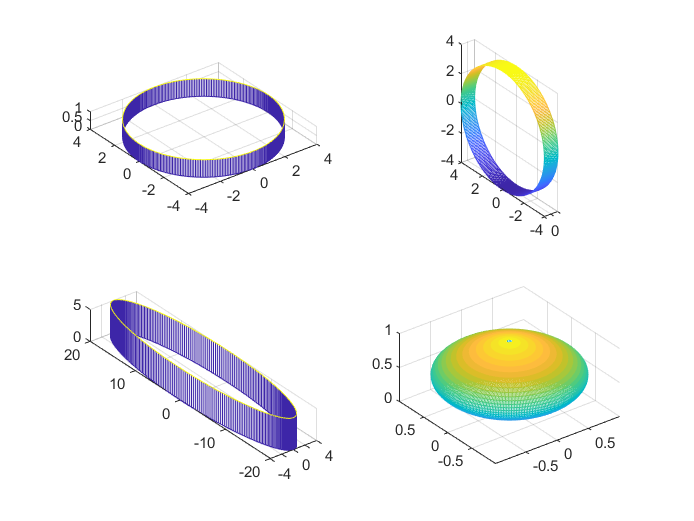
  • sphere 绘制三维球面

    % 生成一个100x100的球体网格数据  
% x, y, z 分别代表网格点的x坐标、y坐标和z坐标  
[x,y,z]=sphere(100);  
    
% 创建一个2x2的子图布局，当前选择第一个子图位置  
subplot(1,2,1)  
    
% 使用mesh函数绘制第一个子图，显示球体的网格结构  
mesh(x,y,z)  
    
% 在当前子图上显示网格线  
grid on  
    
% 设置坐标轴比例相等，使得球体看起来不会变形  
axis equal  
    
% 切换到第二个子图位置  
subplot(1,2,2)  
    
% 绘制球体网格，但x和z坐标分别放大3倍  
% 这将使球体在x和z方向上看起来更大  
mesh(3*x,y,3*z)  
    
% 设置坐标轴比例相等  
axis equal  
    
% 显示网格线  
grid on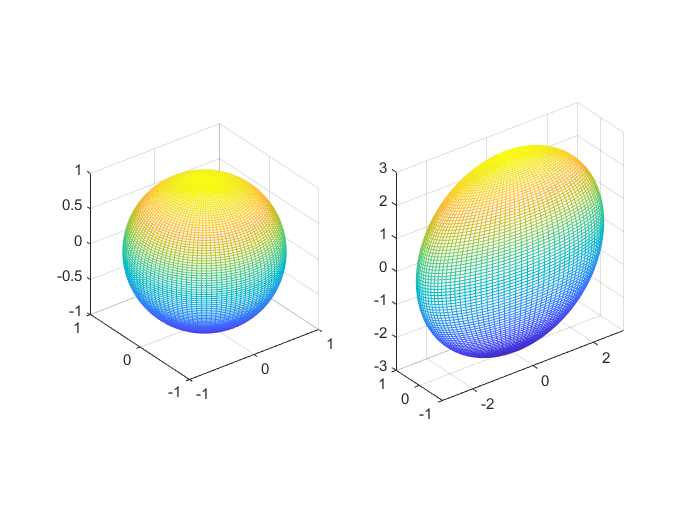

    sphere

  • cylinder 绘制三维柱面

    % 生成一个半径为5，高度为2*pi（即一个完整的圆周长），包含200个网格点的圆柱体数据  
% x, y, z 分别代表网格点的x坐标、y坐标和z坐标  
[x,y,z]=cylinder(4,300);  
    
% 创建一个2x2的子图布局，当前选择第一个子图位置  
subplot(2,2,1)  
% 使用mesh函数绘制第一个子图，显示圆柱体的网格结构  
mesh(x,y,z)   
axis equal  
grid on  
  
subplot(2,2,2)    
% 绘制圆柱体网格，但交换了x和z坐标的位置  
% 这会导致视图沿着对角线翻转，使得原本在x轴上的变化现在显示在z轴上，反之亦然  
mesh(z,y,x)   
axis equal 
grid on  
  
subplot(2,2,3)  
% 绘制圆柱体网格，但y和z坐标都放大5倍  
% 这将使得圆柱体在y和z方向上看起来更大  
mesh(x,5*y,5*z)   
axis equal  
grid on  
  
% 创建一个从0到pi，步长为0.1的向量t  
% 这将用于生成一个基于正弦函数半径变化的圆柱体  
t = 0:0.1:pi;  
% 使用t中的每个值作为半径生成圆柱体，生成的是一个变半径的圆柱体  
% 其中半径随t的正弦值变化，并且仍然包含200个网格点  
[x,y,z]=cylinder(sin(t),300);    
subplot(2,2,4)  
mesh(x,y,z)  
axis equal  
grid on

    cylinder